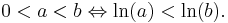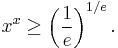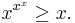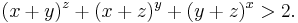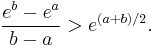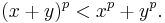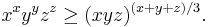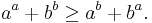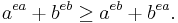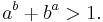Inequality (mathematics)
In mathematics, an inequality is a statement how the relative size or order of two objects, or about whether they are the same or not (See also: equality).
- The notation a < b means that a is less than b.
- The notation a > b means that a is greater than b.
- The notation a ≠ b means that a is not equal to b, but does not say that one is greater than the other or even that they can be compared in size.
In each statement above, a is not equal to b. These relations are known as strict inequalities. The notation a < b may also be read as "a is strictly less than b".
In contrast to strict inequalities, there are two types of inequality statements that are not strict:
- The notation a ≤ b means that a is less than or equal to b (or, equivalently, not greater than b)
- The notation a ≥ b means that a is greater than or equal to b (or, equivalently, not less than b)
An additional use of the notation is to show that one quantity is much greater than another, normally by several orders of magnitude.
- The notation a ≪ b means that a is much less than b. (In measure theory, it denotes instead absolute continuity.)
- The notation a ≫ b means that a is much greater than b.
If the sense of the inequality is the same for all values of the variables for which its members are defined, then the inequality is called an "absolute" or "unconditional" inequality. If the sense of an inequality holds only for certain values of the variables involved, but is reversed or destroyed for other values of the variables, it is called a conditional inequality.
Contents |
Properties
Inequalities are governed by the following properties. Note that, for the transitivity, reversal, addition and subtraction, and multiplication and division properties, the property also holds if strict inequality signs (< and >) are replaced with their corresponding non-strict inequality sign (≤ and ≥).
Transitivity
The transitivity of inequalities states:
- For any real numbers, a, b, c:
- If a > b and b > c; then a > c
- If a < b and b < c; then a < c
- If a > b and b = c; then a > c
- If a < b and b = c; then a < c'[1]
Addition and subtraction
The properties that deal with addition and subtraction state:
- For any real numbers, a, b, c:
- If a < b, then a + c < b + c and a − c < b − c
- If a > b, then a + c > b + c and a − c > b − c
i.e., the real numbers are an ordered group
Multiplication and division
The properties that deal with multiplication and division state:
- For any real numbers, a, b, and non-zero c
More generally this applies for an ordered field, see below.
Additive inverse
The properties for the additive inverse state:
- For any real numbers a and b
- If a < b then −a > −b
- If a > b then −a < −b
Multiplicative inverse
The properties for the multiplicative inverse state:
- For any non-zero real numbers a and b that are both positive or both negative
- If a < b then 1/a > 1/b
- If a > b then 1/a < 1/b
- If either a or b is negative (but not both) then
- If a < b then 1/a < 1/b
- If a > b then 1/a > 1/b
Applying a function to both sides
Any strictly monotonically increasing function may be applied to both sides of an inequality and it will still hold. Applying a strictly monotonically decreasing function to both sides of an inequality means the opposite inequality now holds. The rules for additive and multiplicative inverses are both examples of applying a monotonically decreasing function.
For a non-strict inequality (a ≤ b, a ≥ b):
- Applying a monotonically increasing function preserves the relation (≤ remains ≤, ≥ remains ≥)
- Applying a monotonically decreasing function reverses the relation (≤ becomes ≥, ≥ becomes ≤)
As an example, consider the application of the natural logarithm to both sides of an inequality:
This is true because the natural logarithm is a strictly increasing function.
Ordered fields
If (F, +, ×) is a field and ≤ is a total order on F, then (F, +, ×, ≤) is called an ordered field if and only if:
- a ≤ b implies a + c ≤ b + c;
- 0 ≤ a and 0 ≤ b implies 0 ≤ a × b.
Note that both (Q, +, ×, ≤) and (R, +, ×, ≤) are ordered fields, but ≤ cannot be defined in order to make (C, +, ×, ≤) an ordered field, because −1 is the square of i and would therefore be positive.
The non-strict inequalities ≤ and ≥ on real numbers are total orders. The strict inequalities < and > on real numbers are strict total orders.
Chained notation
The notation a < b < c stands for "a < b and b < c", from which, by the transitivity property above, it also follows that a < c. Obviously, by the above laws, one can add/subtract the same number to all three terms, or multiply/divide all three terms by same nonzero number and reverse all inequalities according to sign. Hence, for example, a < b + e < c is equivalent to a − e < b < c − e.
This notation can be generalized to any number of terms: for instance, a1 ≤ a2 ≤ ... ≤ an means that ai ≤ ai+1 for i = 1, 2, ..., n − 1. By transitivity, this condition is equivalent to ai ≤ aj for any 1 ≤ i ≤ j ≤ n.
When solving inequalities using chained notation, it is possible and sometimes necessary to evaluate the terms independently. For instance to solve the inequality 4x < 2x + 1 ≤ 3x + 2, it is not possible to isolate x in any one part of the inequality through addition or subtraction. Instead, the inequalities must be solved independently, yielding x < 1/2 and x ≥ −1 respectively, which can be combined into the final solution −1 ≤ x < 1/2.
Occasionally, chained notation is used with inequalities in different directions, in which case the meaning is the logical conjunction of the inequalities between adjacent terms. For instance, a < b = c ≤ d means that a < b, b = c, and c ≤ d. This notation exists in a few programming languages such as Python.
Inequalities between means
There are many inequalities between means. For example, for any positive numbers a1, a2, …, an we have H ≤ G ≤ A ≤ Q, where
-
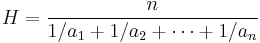
(harmonic mean), ![G = \sqrt[n]{a_1 \cdot a_2 \cdots a_n}](/2012-wikipedia_en_all_nopic_01_2012/I/c4b2be327655964f6682cd4b090a3882.png)
(geometric mean), 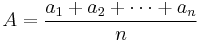
(arithmetic mean), 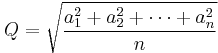
(quadratic mean).
Power inequalities
Sometimes with notation "power inequality" understand inequalities that contain ab type expressions where a and b are real positive numbers or expressions of some variables. They can appear in exercises of mathematical olympiads and some calculations.
Examples
- If x > 0, then
- If x > 0, then
- If x, y, z > 0, then
- For any real distinct numbers a and b,
- If x, y > 0 and 0 < p < 1, then
- If x, y, z > 0, then
- If a, b > 0, then
-
- This inequality was solved by I.Ilani in JSTOR,AMM,Vol.97,No.1,1990.
- If a, b > 0, then
-
- This inequality was solved by S.Manyama in AJMAA,Vol.7,Issue 2,No.1,2010 and by V.Cirtoaje in JNSA,Vol.4,Issue 2,130-137,2011.
- If a, b > 0, then
-
- This result was generalized by R. Ozols in 2002 who proved that if a1, ..., an > 0, then
- (result is published in Latvian popular-scientific quarterly The Starry Sky, see references).
Well-known inequalities
See also list of inequalities.
Mathematicians often use inequalities to bound quantities for which exact formulas cannot be computed easily. Some inequalities are used so often that they have names:
- Azuma's inequality
- Bernoulli's inequality
- Boole's inequality
- Cauchy–Schwarz inequality
- Chebyshev's inequality
- Chernoff's inequality
- Cramér–Rao inequality
- Hoeffding's inequality
- Hölder's inequality
- Inequality of arithmetic and geometric means
- Jensen's inequality
- Kolmogorov's inequality
- Markov's inequality
- Minkowski inequality
- Nesbitt's inequality
- Pedoe's inequality
- Poincaré inequality
- Triangle inequality
Complex numbers and inequalities
The set of complex numbers 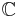 with its operations of addition and multiplication is a field, but it is impossible to define any relation ≤ so that
with its operations of addition and multiplication is a field, but it is impossible to define any relation ≤ so that 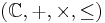 becomes an ordered field. To make
becomes an ordered field. To make 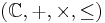 an ordered field, it would have to satisfy the following two properties:
an ordered field, it would have to satisfy the following two properties:
- if a ≤ b then a + c ≤ b + c
- if 0 ≤ a and 0 ≤ b then 0 ≤ a b
Because ≤ is a total order, for any number a, either 0 ≤ a or a ≤ 0 (in which case the first property above implies that 0 ≤ 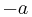 ). In either case 0 ≤ a2; this means that
). In either case 0 ≤ a2; this means that 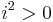 and
and 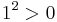 ; so
; so 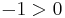 and
and 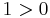 , which means
, which means 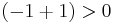 ; contradiction.
; contradiction.
However, an operation ≤ can be defined so as to satisfy only the first property (namely, "if a ≤ b then a + c ≤ b + c"). Sometimes the lexicographical order definition is used:
- a ≤ b if
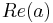 <
< 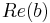 or (
or ( and
and 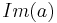 ≤
≤ 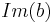 )
)
It can easily be proven that for this definition a ≤ b implies a + c ≤ b + c.
Vector inequalities
Inequality relationships similar to those defined above can also be defined for column vector. If we let the vectors 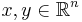 (meaning that
(meaning that 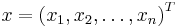 and
and 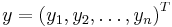 where
where  and
and 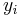 are real numbers for
are real numbers for 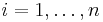 ), we can define the following relationships.
), we can define the following relationships.
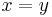 if
if 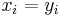 for
for 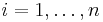
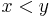 if
if 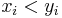 for
for 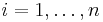
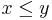 if
if 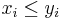 for
for 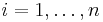 and
and 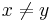
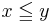 if
if 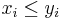 for
for 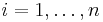
Similarly, we can define relationships for 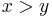 ,
, 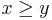 , and
, and 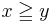 . We note that this notation is consistent with that used by Matthias Ehrgott in Multicriteria Optimization (see References).
. We note that this notation is consistent with that used by Matthias Ehrgott in Multicriteria Optimization (see References).
We observe that the property of Trichotomy (as stated above) is not valid for vector relationships. We consider the case where ![x = \left[ 2, 5 \right]^T](/2012-wikipedia_en_all_nopic_01_2012/I/77efd506bc60a41518cabbb204552c6c.png) and
and ![y = \left[ 3, 4 \right]^T](/2012-wikipedia_en_all_nopic_01_2012/I/4753d9479062cc04a276edeb8ebb842d.png) . There exists no valid inequality relationship between these two vectors. Also, a multiplicative inverse would need to be defined on a vector before this property could be considered. However, for the rest of the aforementioned properties, a parallel property for vector inequalities exists.
. There exists no valid inequality relationship between these two vectors. Also, a multiplicative inverse would need to be defined on a vector before this property could be considered. However, for the rest of the aforementioned properties, a parallel property for vector inequalities exists.
See also
- Binary relation
- Bracket for the use of the < and > signs as brackets
- Fourier-Motzkin elimination
- Inclusion (set theory)
- Inequation
- Interval (mathematics)
- List of inequalities
- Partially ordered set
- Relational operators, used in programming languages to denote inequality
References
- ^ [5,16]
- Hardy, G., Littlewood J.E., Polya, G. (1999). Inequalities. Cambridge Mathematical Library, Cambridge University Press. ISBN 0-521-05206-8.
- Beckenbach, E.F., Bellman, R. (1975). An Introduction to Inequalities. Random House Inc. ISBN 0-394-01559-2.
- Drachman, Byron C., Cloud, Michael J. (1998). Inequalities: With Applications to Engineering. Springer-Verlag. ISBN 0-387-98404-6.
- Murray S. Klamkin. ""Quickie" inequalities" (PDF). Math Strategies. http://ua-mirror.pims.math.ca/pi/issue7/page26-29.pdf.
- Arthur Lohwater (1982). "Introduction to Inequalities". Online e-book in PDF format. http://www.mediafire.com/?1mw1tkgozzu.
- Harold Shapiro (2005,1972–1985). "Mathematical Problem Solving". The Old Problem Seminar. Kungliga Tekniska högskolan. http://www.math.kth.se/math/TOPS/index.html.
- "3rd USAMO". Archived from the original on 2008-02-03. http://web.archive.org/web/20080203070350/www.kalva.demon.co.uk/usa/usa74.html.
- Ehrgott, Matthias (2005). Multicriteria Optimization. Springer-Berlin. ISBN 3-540-21398-8.
- Steele, J. Michael (2004). The Cauchy-Schwarz Master Class: An Introduction to the Art of Mathematical Inequalities. Cambridge University Press. ISBN 978-0521546775. http://www-stat.wharton.upenn.edu/~steele/Publications/Books/CSMC/CSMC_index.html.